그래프에서 노드 사이의 최단 경로를 구하는 알고리즘에는 목적에 따라 여러가지가 있는데, 그 중 하나가 바로 다익스트라 알고리즘이다.

다익스트라는 어떤 하나의 정점에서 다른 모든 노드들까지의 최단 경로를 알려준다.

다만, 그래프의 에지들 중에서 음(-)의 값을 갖는 에지가 있다면 다익스트라를 사용할 수 없다. 즉 모든 에지들이 양의 값을 가져야 한다. 굳이 사용해야 한다면 가장 큰 음의 값을 갖는 가중치만큼을 모든 에지에 더해서 양으로 만들어주자.

그러나 몇몇 특수한 경우들을 제외하고서는 음의 간선이 있을법한 일이 별로 없기 때문에, 최단 경로 문제를 풀기에 대표적이자 기본적인 알고리즘이라고 보면 된다.

개념

다익스트라 알고리즘에서 중요한 기본적인 개념은, 최단 경로의 부분 경로도 최단 경로라는 것이다.

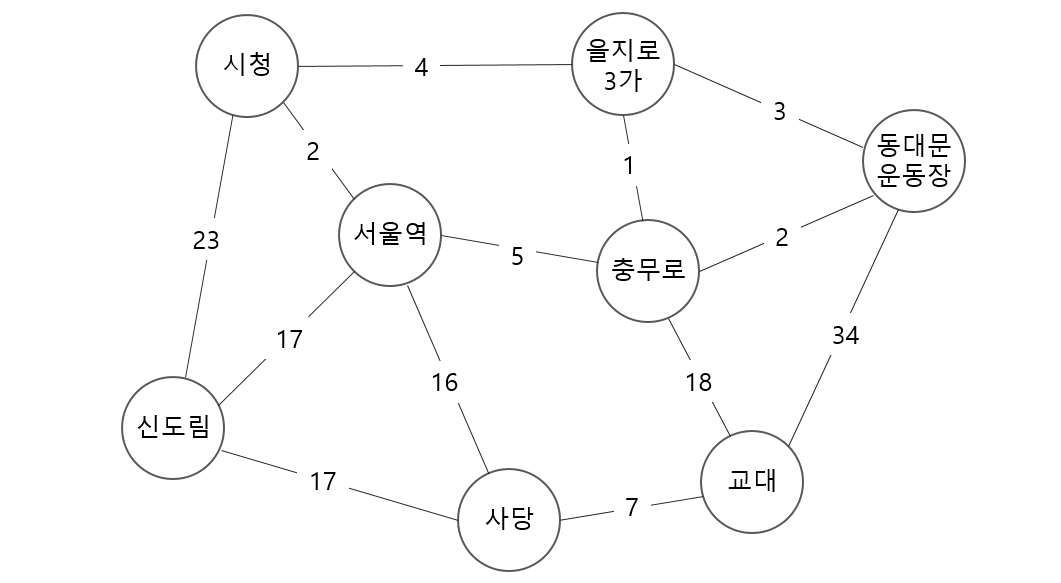
즉, 아래 그림의 신도림에서 동대문운동장까지의 최단 경로는, 아래 중 가장 짧은 경로가 된다.

- 신도림-을지로3가 까지의 최단경로 + 을지로3가-동대문운동장
- 신도림-충무로 까지의 최단경로 + 충무로-동대문운동장
- 신도림-교대 까지의 최단경로 + 교대-동대문운동장

그래프에서 최단 경로로 연결된 기존 노드들의 정보를 사용해 특정 노드의 최단 경로를 구하기 때문에 다이나믹 프로그래밍 문제이기도 하다.

이렇게 노드들을 최단 경로로 연결해나가기 위해서 그래프 탐색 과정이 필요하다.

그래프 탐색 과정

다익스트라는 특정 노드에 인접해 있는 모든 노드들을 탐색한다는 점에서는 BFS 와 비슷하다고 볼 수도 있다.

그러나 에지들에 모두 가중치가 있기 때문에, 노드 a 에서 노드 b 를 탐색했었다고 할지라도, 더 늦게 연결된 노드 c 로부터 노드 b 로 연결된 경로가 더 짧은 경로가 될 수 있다.

따라서 bfs 처럼 방문 여부에 대한 배열로써 중복 탐색을 관리하지 않고, 시작노드로부터 각 지점까지의 최소 거리를 관리함으로써 현재 담겨있는 노드 b 까지 최소거리보다 더 높은 값을 갖는 경로는 탐색하지 않는다.

또한 탐색을 할 때, 단순히 탐색 순서대로 큐에 노드들을 넣게 된다면 (b의 최단 경로를 구하기 위해서 a가 c보다 먼저 큐에 들어왔다면), 더 짧은 거리인 c 가 존재함에도 불구하고 불필요하게 a를 탐색하고 a와 연결된 다른 노드들을 큐에 넣게 된다.

이를 막기 위해 우선순위 큐를 사용하여, 탐색 시 다음 노드를 그 거리와 함께 우선순위 큐에 넣어줌으로써 현재 상황에서 시작노드로부터 가장 가까운 노드 순서대로 탐색할 수 있다.

시작노드부터의 거리가 작은 순으로 우선순위 큐에 담게 됨으로써 홉 수가 아닌 최단 경로 순으로 탐색을 할 수 있고, 따라서 노드 b까지 여러 노드들을 거쳐 왔더라도 더 가중치가 낮기 때문에 우선순위 큐에 먼저 들어가게 되어 탐색되는 것이다.

요약하자면, 우선순위 큐를 사용함으로써, (최단 경로로 연결된 현재 노드에서 연결된 새로운 노드들 과 우선순위 큐에 들어있는 다른 노드로부터 연결되어있는 노드들) 중에 가장 가까운(최단 경로인) 노드 순서대로 탐색할 수 있기 때문에, 모든 노드들에 대한 최단 경로를 구할 수 있다.

파이썬 코드

import heapq

def dijkstra(start, graph, INF):
    # distance[i] 는, start 에서 i 까지의 최단 거리를 담음
    distance = [INF for _ in range(len(graph))]
    pq = []
    # start 지점부터 pq 에 넣고 출발
    distance[start] = 0
    heapq.heappush(pq, (0, start))

    # 우선순위 큐가 빌 때 까지
    while len(pq) > 0:
        # 노드 하나를 꺼내서 확인
        cur_dist, cur_node = heapq.heappop(pq)
        # 만약 해당 노드까지의 거리가 현재 저장된 최단거리보다 크다면 그냥 종료
        if cur_dist > distance[cur_node]:
            continue
        # 해당 노드에 연결되어있는 모든 인접 노드들 탐색
        for next_node, next_dist in graph[cur_node]:
            # 만약 연결된 노드들 중에 그 노드까지의 최단거리를 갱신할 수 있는 경로가 발견되면
            if cur_dist + next_dist < distance[next_node]:
                # 최단 거리 갱신 후
                distance[next_node] = cur_dist + next_dist
                # 해당 경로를 다시 pq 에 넣어줘서 연결될 수 있는 또다른 최단경로들 탐색
                heapq.heappush(pq, (distance[next_node], next_node))
    
    # start 부터 다른 정점들까지의 최단 거리들 반환
    return distance

예시

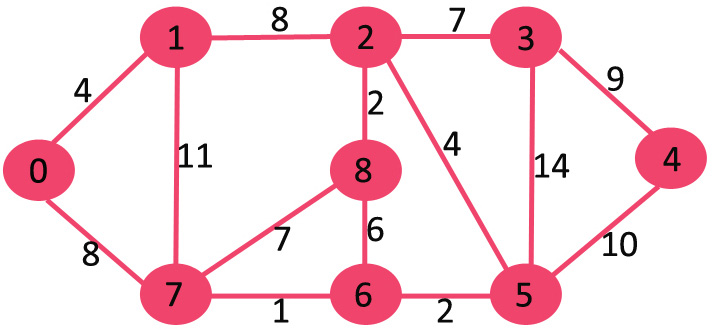
1. 각 노드까지의 최단거리 값을 담고 있는 배열을 INF(연결되지 않았다는 표시로 아주 큰 값을 넣음)로 초기화시켜준다.

2. 시작 노드가 0 이라고 한다면, 우선순위 큐에 0 을 넣고 탐색을 시작한다.

3. 처음에는 0 에 연결된 1 과 7 노드를 확인하는데, 둘 다 INF 보다 거리가 짧기 때문에 distance[1] 의 값은 4가 되고, distance[7]의 값은 8이 된다.

4. 우선순위 큐에는 해당 노드까지의 최단거리도 같이 넣고 거리를 기준으로 정렬시키기 때문에, 다음 탐색에서는 현재 최단 경로인 노드 1을 탐색한다.

5. 노드 1에 연결된 노드 0, 노드 2, 노드7을 탐색하는데, 노드 2의 경우는 최단경로를 갱신할 수 있기 때문에 우선순위 큐에 경로의 길이인 12로 하여 넣어주지만, 노드 7의 경우는 기존 거리인 8보다 현재 거리 15가 더 크기 때문에 우선순위 큐에 넣지 않는다(노드 0도 마찬가지).

6. 따라서 현재 우선순위 큐에는 노드 7(거리 8), 노드 2(거리 12) 두개가 들어있고, 다음 탐색은 노드 7이 된다.

7. 노드 7에서는 자기와 연결된 노드 0, 노드 8, 노드 6을 탐색한다. 노드 0은 되돌아가는 것이기 때문에 당연히 기존 거리보다 더 멀어지게 되므로 노드 1에서와 마찬가지로 큐에 넣지 않고, 나머지 두 노드는 모두 첫 탐색이므로 우선순위 큐에 각각의 거리와 함께 넣어준다.

8. 현재 우선순위 큐에는 노드 6(거리 9), 노드 2(거리 12), 노드 8(거리 15)가 담겨있으므로, 다음 탐색은 노드 6이 된다.

9. 노드 6도 마찬가지로 자기와 연결된 노드 7, 노드 8, 노드 5를 탐색하지만, 새롭게 최단거리를 갱신할 수 있는 노드 5만 우선순위 큐에 넣어주고 종료한다.

이런 식으로 현재의 최단경로에서 만들 수 있는 다른 최단경로를 하나씩 구해나가며, 모든 노드가 탐색되기까지 반복한다.