그래프에서 시작 노드가 주어지고, 해당 정점에서 그래프에 있는 다른 모드 노드들까지의 최단 경로를 찾는 문제가 있다고 하자.

모든 간선의 가중치가 1인 경우 너비 하나를 탐색할때마다 거리가 1씩 증가한다고 볼 수 있기 때문에, 특정 노드까지의 최단거리를 구할 때 BFS를 활용할 수 있다.

이 때 말하는 너비란, 아래 그림과 같이 시작 노드(1)를 루트로 잡고 트리 형태로 쭉 끌어당겼을 때, 트리에서의 depth 하나를 뜻한다.

1번 노드는 2번 노드와 3번 노드에만 연결되어 있기 때문에, 시작 노드인 1번을 기준으로 했을 때 다음에 탐색할 너비에 속하는 노드들은 2번과 3번이 된다.

그리고 2번 노드 입장에서 봤을 때, 자신은 현재 너비 1에 속해 있기 때문에, 자신이 연결하고 있는 다음 너비들은 자신의 너비 + 1 에 속한다고 할 수 있다.

그렇게 4번과 5번 노드가 두번째 너비에 포함되어 탐색되고, 3번 노드 기준으로 봤을 때 마찬가지로 자신에게 연결된 다음 노드들을 두번째 너비에 포함시킨다.(6번, 7번)

결과적으로 그래프에 포함되어 있는 모든 노드들을 탐색하는 과정에서, 마치 바이러스가 여러 사람에게 퍼지고, 또 그 사람들이 다른 여러 사람들에게 퍼지듯이 동작한다.

그러나 그래프가 항상 단방향 트리 형태로 구성되는 것이 아니기 때문에, 양방향으로 연결되는 경우 역시 고려해야 한다.

만약 양방향으로 연결되어있을 경우에는, 두 노드 간에 다음 너비를 탐색하는 과정에서 서로가 서로를 계속해서 포함시킬 것이므로 무한 루프에 빠지게 된다.

따라서, N개 노드에 대해서 해당 노드를 방문했는지 여부를 확인할 수 있는 배열을 하나 두고, 노드를 탐색할 때 마다 이 배열을 갱신시켜줌으로써 중복 방문을 제거한다.

현재 노드에서 다음 너비에 있는 노드들 중에, 지금까지 방문한 적 없는 노드만을 다음 너비의 후보로 추가하면 모든 노드들 한번씩만 탐색하여 O(N)을 만들 수 있다.

코드

def bfs(graph, start):
    # 중복 방문을 피하기 위한 배열
    visited = [False for _ in range(len(graph))]
    visited[start] = True
    order = []

    # 큐에 시작노드를 넣은 뒤 탐색 시작
    q = [start]
    while len(q) > 0:
        # 다음 너비를 위한 큐
        nq = []
        # 현재 너비의 큐에 담긴 노드들을 하나씩 검사하며
        for cur in q:
            order.append(cur)
            # 자신에게 연결된 다음 너비의 노드들을 확인하는데,
            for nxt in graph[cur]:
                # 만약 방문하지 않았던 노드일 경우에는 다음 너비에 추가
                if not visited[nxt]:
                    visited[nxt] = True
                    nq.append(nxt)
        # 다음 반복때 사용할 큐를 nq 로 바꿔줌으로써 다음 너비를 탐색
        q = nq
    return order

예시

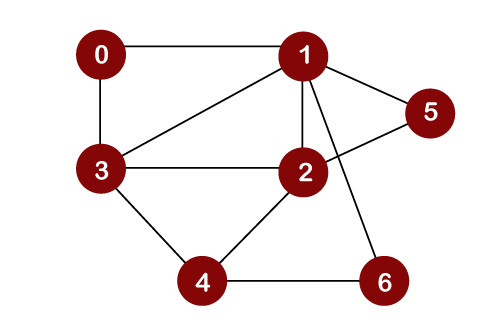
1. BFS를 0번 노드부터 시작한다고 했을 때, 큐에는 [0] 만이 담기게 되고, 0번 노드에 연결된 1번과 3번노드만이 너비 1에 해당하기 때문에 해당 노드들을 다음 큐(nq)에 추가해준다.

2. 추가하는 과정에서, 어차피 이후에 다른 노드에서 1번과 3번을 탐색하면 안되기 때문에 visited 배열을 갱신해준다.

3. 이번 너비를 모두 탐색했다면, 탐색에서 사용할 큐(q)를 다음 너비의 큐(nq)로 바꿔줌으로써 다음 반복 때 자연스럽게 다음 너비에 담긴 노드들을 검사하게 해준다.

4. 현재 큐에는 [1, 3] 이 들어있기 때문에, 각각의 노드들과 연결된 그 다음 너비를 다시 찾아준다.

5. 1번 노드는 0,2,3,5,6 과 연결되어있지만, 0번노드와 3번노드는 이전 탐색들에서 이미 방문처리 되었기 때문에, 다음 너비로써 추가하지 않고 새롭게 연결되는 2,5,6 노드만 nq 에 추가해준다.

6. 마찬가지로 3번 노드는 0,1,2,4 와 연결되어있고, 0번노드와 1번노드는 이전 탐색들에서 방문처리 되었고, 2번 노드는 앞서 1번노드를 검사해줄 때 nq에 이미 추가되면서 방문되었기 때문에 4번 노드 하나만 추가해준다.

7. 현재 nq에는 [2, 5, 6, 4]가 담겨있고, 다음 너비에서 해당 노드들을 탐색할 수 있게 q=nq 를 통해 교체해준다.

8. 큐에 담긴 2,5,6,4 노드들을 모두 검사하는데, 각 노드별로 연결된 다음 노드들이 이미 모두 방문처리 된 노드이기 때문에 nq에는 더이상 노드가 추가되지 않고, 이대로 반복은 종료된다.

9. 결과적으로 너비별로 노드들을 탐색한 순서는 0-1-3-2-5-6-4가 되며(물론 같은 너비 안에서의 탐색 순서는 크게 중요하지 않음), 각 노드들의 너비는 0, 1, 2, 1, 2, 2, 2라고 볼 수 있다.